
The reason has to involve the way that counting arose in the Sumerian civilisation, just as 10 became a base in other civilisations who began counting on their fingers, and twenty became a base for those who counted on both their fingers and toes. Can you imagine the Sumerians setting set up a committee to decide on their number base - no things just did not happen in that way. I just do not believe that anyone ever chose a number base for any civilisation. Perhaps I've set up my own argument a little, but the phrase "choosing 60 as a base" which I just used is highly significant. I feel that all of these reasons are really not worth considering seriously. Notice this argument almost contradicts itself since it assumes 10 as the basic unit for division! Now there are sixty of these basic units in a circle so again we have the proposed reason for choosing 60 as a base. Now an angle of an equilateral triangle is 60° so if this were divided into 10, an angle of 6° would become the basic angular unit. For example one theory is that an equilateral triangle was considered the fundamental geometrical building block by the Sumerians. Another hypothesis concerns the fact that the sun moves through its diameter 720 times during a day and, with 12 Sumerian hours in a day, one can come up with 60. Again the idea is not that convincing since the Sumerians certainly knew that the year was longer than 360 days. That the year was thought to have 360 days was suggested as a reason for the number base of 60 by the historian of mathematics Moritz Cantor. The suggestion that 60 is the product of the number of months in the year (moons per year ) with the number of planets (Mercury, Venus, Mars, Jupiter, Saturn ) again seems far fetched as a reason for base 60. Several theories have been based on astronomical events. However although Neugebauer may be correct, the counter argument would be that the system of weights and measures was a consequence of the number system rather than visa versa.

For example the decimal 12345 representsġ × 6 0 3 + 57 × 6 0 2 + 46 × 60 + 40 1 \times 60^\normalsize 3 2 as basic fractions. Now given a positional system one needs a convention concerning which end of the number represents the units. Here are the 59 symbols built from these two symbols

This is because the 59 numbers, which go into one of the places of the system, were built from a 'unit' symbol and a 'ten' symbol. Now although the Babylonian system was a positional base 60 system, it had some vestiges of a base 10 system within it. However, rather than have to learn 10 symbols as we do to use our decimal numbers, the Babylonians only had to learn two symbols to produce their base 60 positional system.

Now of course this comment is based on knowledge of our own decimal system which is a positional system with nine special symbols and a zero symbol to denote an empty place.
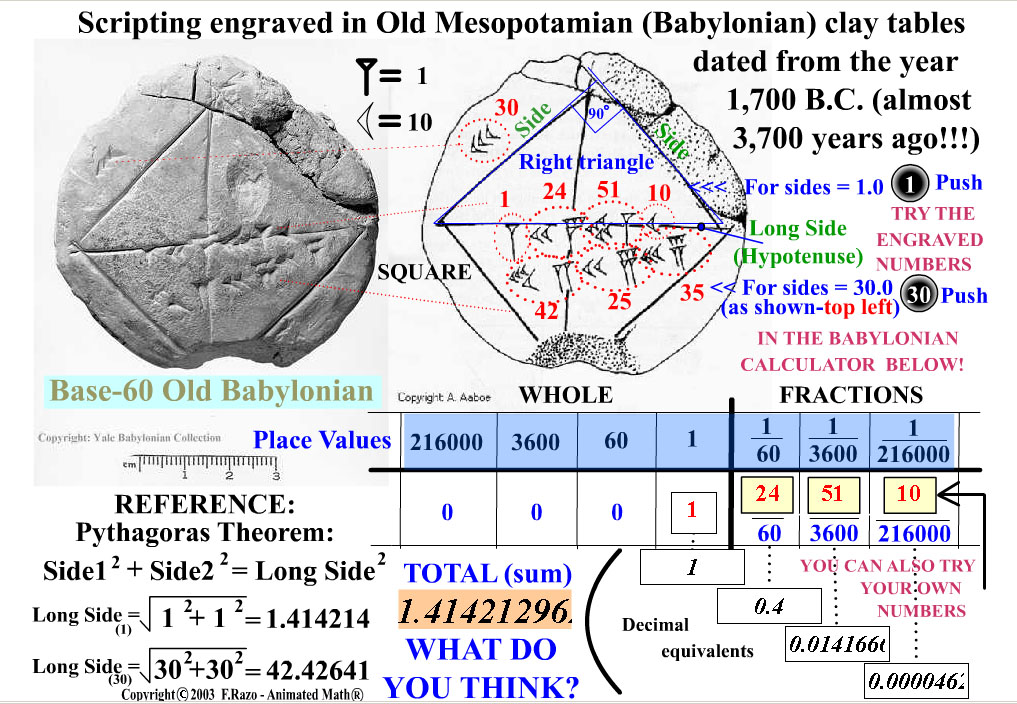
Often when told that the Babylonian number system was base 60 people's first reaction is: what a lot of special number symbols they must have had to learn. Some would argue that it was their biggest achievement in mathematics. Yet neither the Sumerian nor the Akkadian system was a positional system and this advance by the Babylonians was undoubtedly their greatest achievement in terms of developing the number system. From the number systems of these earlier peoples came the base of 60, that is the sexagesimal system. Certainly in terms of their number system the Babylonians inherited ideas from the Sumerians and from the Akkadians. We give a little historical background to these events in our article Babylonian mathematics.


 0 kommentar(er)
0 kommentar(er)
